Last week, I talked about six recent papers from our group, and discussed the first two in detail. This week, I'll discuss the remaining four. They fall into two categories: robustness, and science of ML.
Robustness
By robustness, I mean both making systems less likely to fail in new situations, and being able to predict when and how they will fail. Our three papers address different aspects of this: the first seeks to automatically estimate a model’s performance in a new situation, the second seeks to understand in what way open-ended generation systems fail, and the third provides a training procedure that improves robustness along several dimensions.
Predicting Out-of-Distribution Error. Yaodong Yu, Zitong Yang, and Alex Wei sought to solve the following problem: given a classifier $\theta$ trained on a distribution $p_{\mathrm{in}}$, and given sample inputs from a new distribution $p_{\mathrm{out}}$, can we predict how well $\theta$ works on the new distribution $p_{\mathrm{out}}$? For instance, maybe an image classifier was trained on images in the US ($p_{\mathrm{in}}$), and we want to know how well it will do on images in France ($p_{\mathrm{out}}$). Since we have no output labels for $p_{\mathrm{out}}$, this is an unsupervised estimation problem.
There are a number of heuristics for predicting out-of-distribution error, such as looking at the model's confidence or the disagreement rate between multiple models with different random seeds. However, most of these heuristics have the same problem: they are insensitive to changes that are orthogonal to the training manifold. As a result, they tend to fail on “hard” distribution shifts—for instance, given a distribution of adversarial examples, they all predict the model will have high accuracy.
We present a new method, ProjNorm, that does well on hard distribution shifts. For instance, compared to ATC (a strong existing method), we make more accurate predictions when the error is large:
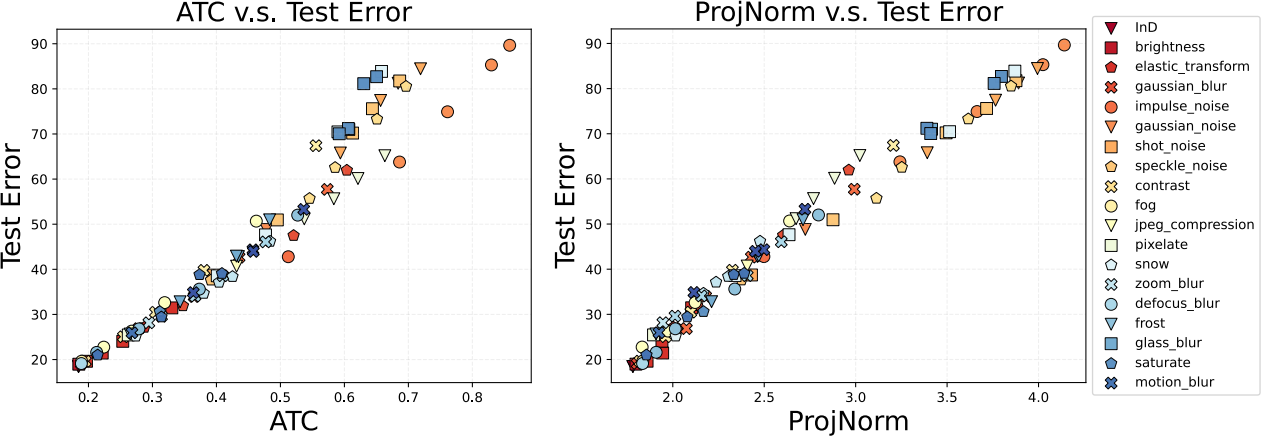
The method is simple, but it takes a bit of time (for me at least!) to grasp the intuition, so I’ll leave that for the paper. But basically, you use the model $\theta$ to pseudo-label the samples from $p_{\mathrm{out}}$, fine-tune a model on those pseudo-labels, and then compare that new model to $\theta$. It turns out that this can be interpreted as a nonlinear projection operator and overcomes the problems with previous methods.
Why you should care. Many of the ways that ML models could fail come from generalizing poorly. For instance, a system might learn an objective function that generates good behavior in one situation, but the wrong behavior in new situations. Detecting these failures automatically would be very useful if we could do so reliably. Doing so could be very hard in general, and I’d say the jury is very much still out, but this paper has made me more optimistic that it’s possible to do something nontrivial and interesting.
Capturing Failures of Large Language Models. Most work on robustness focuses on classification error rates–how much more often a model gets the answer wrong when presented with unusual or out-of-distribution of inputs. However, modern language models are open-ended: rather than a class label, they generate arbitrary text. So to understand how they behave on unusual inputs, it’s not enough to just understand the error rate. For instance, one language model might err by producing gibberish, while another responds with insults or other toxic text. Or a code model could either produce code that doesn’t compile, or code that deletes all files in the home directory.
To tame the complexity of open-ended generation, Erik Jones used human cognitive biases to taxonomize and test a subset of possible failure modes. For instance, the framing and anchoring biases led us to hypothesize that when incorrect code appears in a model’s context, similar code will appear in the outputs to new prompts. We design experiments to test and quantify how often this occurs, and find that it is indeed common. Inspired by these and other cognitive biases, we unearth several new types of failure modes that code generation models are prone to.
Why you should care. In my opinion, robustness is most important in what I’ll call “structured output” settings—where the output is a complex object such as a sentence, a trajectory, or a computer program, rather than just a class label. The reason to care about these settings is twofold: first, the cost of failures is potentially much larger—the maximum damage I can do with a computer program is greater than the maximum damage I can do with a class label. Second, some important classes of failures, such as objective misgeneralization, only show up in structured output settings. Our work provides useful approaches for finding robustness failures in these structured output settings.
Comprehensively Improving Safety Measures. Dan Hendrycks, Andy Zou, and several other collaborators designed a new data augmentation strategy called PixMix, which is partly inspired by Kataoka et al.’s observation that fractals are an effective source of pretraining images.
PixMix works by repeatedly mixing with a high-complexity image (such as a fractal) and then applying a standard augmentation such as posterization. Two resulting example images are shown below:

While PixMix does not improve accuracy more than other data augmentation methods, it helps significantly more with many safety properties, such as calibration, anomaly detection, robustness to corruptions, and robustness to adversaries.
Why you should care. PixMix takes a different perspective from other data augmentation strategies. Rather than trying to maximize the entropy or the diversity of the augmented images, it seeks to maximize their complexity. In general, complexity feels like an important and understudied concept for AI safety. For instance, it seems plausible to me that what is most important for controlling an AI system’s behavior is the complexity of its supervision signal—supervision that is not complex enough will not pin down the behavior in enough cases. In another direction, the simplest case for AI posing risks is that it is a complex self-organizing system, and most such systems are difficult to control and create unintended consequences. Given the potential importance of complexity, I’m excited to see it used to make ML systems safer.
Science of ML
“Science of ML” is a fairly broad term, but for me it means trying to understand laws that govern neural network behavior, such that we can predict that behavior in new situations. One particular use case is for forecasting—predicting what will happen as we make neural nets bigger and train them on more data.
Predicting How Real-World Representations Generalize. Alex Wei and Wei Hu improved our understanding of neural networks, by identifying a mathematical framework that helps clarify neural scaling laws, as well as the role of pretraining.
Because neural networks are difficult to analyze, we studied linear models derived from neural networks. Specifically, given a trained neural network, you can take a first-order Taylor approximation in parameter space to obtain a linear model, which will usually have more parameters than the number of data points (since most neural networks are overparameterized). As a result, we treat the model as a nonparametric (kernel) model, which we call the empirical neural tangent kernel (eNTK). We can check empirically that while eNTKs don’t perform as well as neural networks, they do much better than traditional NTK models (which are obtained from random rather than trained networks). The eNTK models also exhibit power law scaling just like regular neural networks do.
We might therefore hope that understanding eNTKs will help us to understand neural networks. To help with this, Alex and Wei set out to understand the generalization error of neural networks (the error on fresh test samples after the model has been trained on N training samples). It turns out that the generalization error can be effectively predicted by a function called the generalized cross-validation estimator (GCV), and that this can be mathematically justified in terms of random matrix laws. More interestingly, the GCV estimator predicts that the error depends primarily on two terms: the effective dimension, and the alignment between the eNTK features and the true function we want to learn. Both of these terms are needed to accurately predict neural scaling laws, and they are also needed to understand pretraining. For instance, pretrained models actually have larger effective dimension (contrary to my initial intuition), and are better primarily because they have much better alignment with the true function.
Why you should care. Neural scaling laws are a promising avenue to help forecast the behavior of future ML models. However, the reason they arise is still not fully understood. This is important because I expect we will need to deal with much more complex scaling laws in the future, such as the joint scaling between a policy model and a reward model when learning reward functions from human feedback. It may be too expensive to exhaustively map out these laws empirically, and theoretical understanding can help us reach the right answer more efficiently. I think Alex and Wei’s work brings us a step closer to doing that.
