Model Mis-specification and Inverse Reinforcement Learning

In my previous post, “Latent Variables and Model Mis-specification”, I argued that while machine learning is good at optimizing accuracy on observed signals, it has less to say about correctly inferring the values for unobserved variables in a model. In this post I’d like to focus in on a specific context for this: inverse reinforcement learning (Ng et al. 2000, Abeel et al. 2004, Ziebart et al. 2008, Ho et al 2016), where one observes the actions of an agent and wants to infer the preferences and beliefs that led to those actions. For this post, I am pleased to be joined by Owain Evans, who is an active researcher in this area and has co-authored an online book about building models of agents (see here in particular for a tutorial on inverse reinforcement learning and inverse planning).

Owain and I are particularly interested in inverse reinforcement learning (IRL) because it has been proposed (most notably by Stuart Russell) as a method for learning human values in the context of AI safety; among other things, this would eventually involve learning and correctly implementing human values by artificial agents that are much more powerful, and act with much broader scope, than any humans alive today. While we think that overall IRL is a promising route to consider, we believe that there are also a number of non-obvious pitfalls related to performing IRL with a mis-specified model. The role of IRL in AI safety is to infer human values, which are represented by a reward function or utility function. But crucially, human values (or human reward functions) are never directly observed.

Below, we elaborate on these issues. We hope that by being more aware of these issues, researchers working on inverse reinforcement learning can anticipate and address the resulting failure modes. In addition, we think that considering issues caused by model mis-specification in a particular concrete context can better elucidate the general issues pointed to in the previous post on model mis-specification.

Specific Pitfalls for Inverse Reinforcement Learning

In “Latent Variables and Model Mis-specification”, Jacob talked about model mis-specification, where the “true” model does not lie in the model family being considered. We encourage readers to read that post first, though we’ve also tried to make the below readable independently.

In the context of inverse reinforcement learning, one can see some specific problems that might arise due to model mis-specification. For instance, the following are things we could misunderstand about an agent, which would cause us to make incorrect inferences about the agent’s values:

The actions of the agent. If we believe that an agent is capable of taking a certain action, but in reality they are not, we might make strange inferences about their values (for instance, that they highly value not taking that action). Furthermore, if our data is e.g. videos of human behavior, we have an additional inference problem of recognizing actions from the frames.
The information available to the agent. If an agent has access to more information than we think it does, then a plan that seems irrational to us (from the perspective of a given reward function) might actually be optimal for reasons that we fail to appreciate. In the other direction, if an agent has less information than we think, then we might incorrectly believe that they don’t value some outcome A, even though they really only failed to obtain A due to lack of information.
The long-term plans of the agent. An agent might take many actions that are useful in accomplishing some long-term goal, but not necessarily over the time horizon that we observe the agent. Inferring correct values thus also requires inferring such long-term goals. In addition, long time horizons can make models more brittle, thereby exacerbating model mis-specification issues.

There are likely other sources of error as well. The general point is that, given a mis-specified model of the agent, it is easy to make incorrect inferences about an agent’s values if the optimization pressure on the learning algorithm is only towards predicting actions correctly in-sample.

In the remainder of this post, we will cover each of the above aspects -- actions, information, and plans -- in turn, giving both quantitative models and qualitative arguments for why model mis-specification for that aspect of the agent can lead to perverse beliefs and behavior. First, though, we will briefly review the definition of inverse reinforcement learning and introduce relevant notation.

Inverse Reinforcement Learning: Definition and Notations

In inverse reinforcement learning, we want to model an agent taking actions in a given environment. We therefore suppose that we have a state space $S$ (the set of states the agent and environment can be in), an action space $A$ (the set of actions the agent can take), and a transition function $T(s' \mid s,a)$, which gives the probability of moving from state $s$ to state $s'$ when taking action $a$. For instance, for an AI learning to control a car, the state space would be the possible locations and orientations of the car, the action space would be the set of control signals that the AI could send to the car, and the transition function would be the dynamics model for the car. The tuple of $(S,A,T)$ is called an $MDP\backslash R$, which is a Markov Decision Process without a reward function. (The $MDP\backslash R$ will either have a known horizon or a discount rate $\gamma$ but we’ll leave these out for simplicity.)

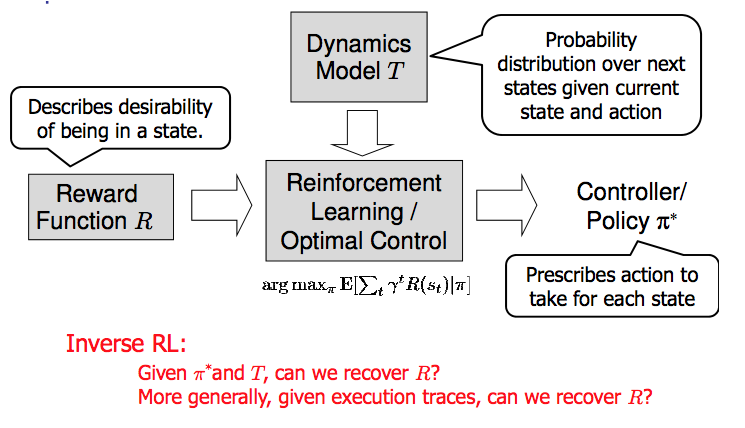
Figure 1: Diagram showing how IRL and RL are related. (Credit: Pieter Abbeel’s slides on IRL)

The inference problem for IRL is to infer a reward function $R$ given an optimal policy $\pi^* : S \to A$ for the $MDP\backslash R$ (see Figure 1). We learn about the policy $\pi^*$ from samples $(s,a)$ of states and the corresponding action according to $\pi^*$ (which may be random). Typically, these samples come from a trajectory, which records the full history of the agent’s states and actions in a single episode:

$(s_0, a_0), (s_1, a_1), \ldots, (s_n, a_n) $

In the car example, this would correspond to the actions taken by an expert human driver who is demonstrating desired driving behaviour (where the actions would be recorded as the signals to the steering wheel, brake, etc.).

Given the $MDP\backslash R$ and the observed trajectory, the goal is to infer the reward function $R$. In a Bayesian framework, if we specify a prior on $R$ we have:

$P(R \mid s_{0:n},a_{0:n}) \propto P( s_{0:n},a_{0:n} \mid R) P(R) = P(R) \cdot \prod_{i=0}^n P( a_i \mid s_i, R)$

The likelihood $P(a_i \mid s_i, R)$ is just $\pi_R(s)[a_i]$, where $\pi_R$ is the optimal policy under the reward function $R$. Note that computing the optimal policy given the reward is in general non-trivial; except in simple cases, we typically approximate the policy using reinforcement learning (see Figure 1). Policies are usually assumed to be noisy (e.g. using a softmax instead of deterministically taking the best action). Due to the challenges of specifying priors, computing optimal policies and integrating over reward functions, most work in IRL uses some kind of approximation to the Bayesian objective (see the references in the introduction for some examples).

Recognizing Human Actions in Data

IRL is a promising approach to learning human values in part because of the easy availability of data. For supervised learning, humans need to produce many labeled instances specialized for a task. IRL, by contrast, is an unsupervised/semi-supervised approach where any record of human behavior is a potential data source. Facebook's logs of user behavior provide trillions of data-points. YouTube videos, history books, and literature are a trove of data on human behavior in both actual and imagined scenarios. However, while there is lots of existing data that is informative about human preferences, we argue that exploiting this data for IRL will be a difficult, complex task with current techniques.

Inferring Reward Functions from Video Frames

As we noted above, applications of IRL typically infer the reward function R from observed samples of the human policy $\pi^*$. Formally, the environment is a known $MDP\backslash R = (S,A,T)$ and the observations are state-action pairs, $(s,a) \sim pi^*$. This assumes that (a) the environment’s dynamics $T$ are given as part of the IRL problem, and (b) the observations are structured as “state-action” pairs. When the data comes from a human expert parking a car, these assumptions are reasonable. The states and actions of the driver can be recorded and a car simulator can be used for $T$. For data from YouTube videos or history books, the assumptions fail. The data is a sequence of partial observations: the transition function $T$ is unknown and the data does not separate out state and action. Indeed, it’s a challenging ML problem to infer human actions from text or videos.

Movie still: What actions are being performed in this situation? (Source)

As a concrete example, suppose the data is a video of two co-pilots flying a plane. The successive frames provide only limited information about the state of the world at each time step and the frames often jump forward in time. So it’s more like a POMDP with a complex observation model. Moreover, the actions of each pilot need to be inferred. This is a challenging inference problem, because actions can be subtle (e.g. when a pilot nudges the controls or nods to his co-pilot).

To infer actions from observations, some model relating the true state-action $(s,a)$ to the observed video frame must be used. But choosing any model makes substantive assumptions about how human values relate to their behavior. For example, suppose someone attacks one of the pilots and (as a reflex) he defends himself by hitting back. Is this reflexive or instinctive response (hitting the attacker) an action that is informative about the pilot’s values? Philosophers and neuroscientists might investigate this by considering the mental processes that occur before the pilot hits back. If an IRL algorithm uses an off-the-shelf action classifier, it will lock in some (contentious) assumptions about these mental processes. At the same time, an IRL algorithm cannot learn such a model because it never directly observes the mental processes that relate rewards to actions.

Inferring Policies From Video Frames

When learning a reward function via IRL, the ultimate goal is to use the reward function to guide an artificial agent’s behavior (e.g. to perform useful tasks to humans). This goal can be formalized directly, without including IRL as an intermediate step. For example, in Apprenticeship Learning, the goal is to learn a “good” policy for the $MDP\backslash R$ from samples of the human’s policy $\pi^*$ (where $\pi^*$ is assumed to approximately optimize an unknown reward function). In Imitation Learning, the goal is simply to learn a policy that is similar to the human’s policy.

Like IRL, policy search techniques need to recognize an agent’s actions to infer their policy. So they have the same challenges as IRL in learning from videos or history books. Unlike IRL, policy search does not explicitly model the reward function that underlies an agent’s behavior. This leads to an additional challenge. Humans and AI systems face vastly different tasks and have different action spaces. Most actions in videos and books would never be performed by a software agent. Even when tasks are similar (e.g. humans driving in the 1930s vs. a self-driving car in 2016), it is a difficult transfer learning problem to use human policies in one task to improve AI policies in another.

IRL Needs Curated Data

We argued that records of human behaviour in books and videos are difficult for IRL algorithms to exploit. Data from Facebook seems more promising: we can store the state (e.g. the HTML or pixels displayed to the human) and each human action (clicks and scrolling). This extends beyond Facebook to any task that can be performed on a computer. While this covers a broad range of tasks, there are obvious limitations. Many people in the world have a limited ability to use a computer: we can’t learn about their values in this way. Moreover, some kinds of human preferences (e.g. preferences over physical activities) seem hard to learn about from behaviour on a computer.

Information and Biases

Human actions depend both on their preferences and their beliefs. The beliefs, like the preferences, are never directly observed. For narrow tasks (e.g. people choosing their favorite photos from a display), we can model humans as having full knowledge of the state (as in an MDP). But for most real-world tasks, humans have limited information and their information changes over time (as in a POMDP or RL problem). If IRL assumes the human has full information, then the model is mis-specified and generalizing about what the human would prefer in other scenarios can be mistaken. Here are some examples:

(1). Someone travels from their house to a cafe, which has already closed. If they are assumed to have full knowledge, then IRL would infer an alternative preference (e.g. going for a walk) rather than a preference to get a drink at the cafe.

(2). Someone takes a drug that is widely known to be ineffective. This could be because they have a false belief that the drug is effective, or because they picked up the wrong pill, or because they take the drug for its side-effects. Each possible explanation could lead to different conclusions about preferences.

(3). Suppose an IRL algorithm is inferring a person's goals from key-presses on their laptop. The person repeatedly forgets their login passwords and has to reset them. This behavior is hard to capture with a POMDP-style model: humans forget some strings of characters and not others. IRL might infer that the person intends to repeatedly reset their passwords.

Example (3) above arises from humans forgetting information -- even if the information is only a short string of characters. This is one way in which humans systematically deviate from rational Bayesian agents. The field of psychology has documented many other deviations. Below we discuss one such deviation -- time-inconsistency -- which has been used to explain temptation, addiction and procrastination.

Time-inconsistency and Procrastination

An IRL algorithm is inferring Alice’s preferences. In particular, the goal is to infer Alice’s preference for completing a somewhat tedious task (e.g. writing a paper) as opposed to relaxing. Alice has $T$ days in which she could complete the task and IRL observes her working or relaxing on each successive day.

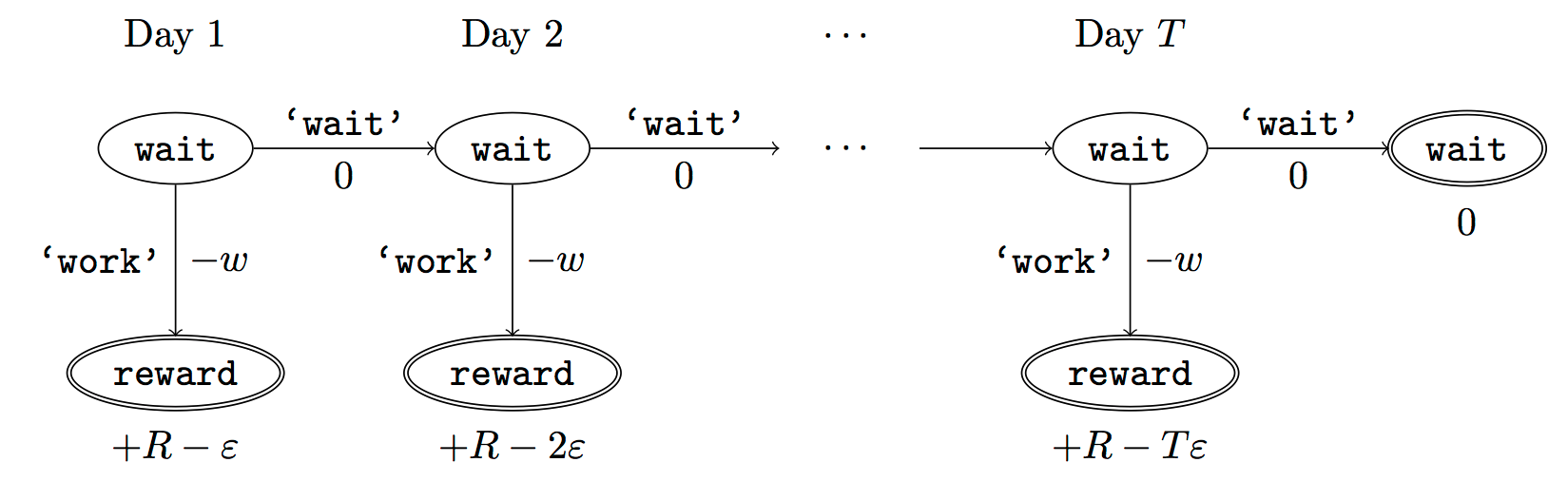
Figure 2. MDP graph for choosing whether to “work” or “wait” (relax) on a task.

Formally, let R be the preference/reward Alice assigns to completing the task. Each day, Alice can “work” (receiving cost $w$ for doing tedious work) or “wait” (cost $0$). If she works, she later receives the reward $R$ minus a tiny, linearly increasing cost (because it’s better to submit a paper earlier). Beyond the deadline at $T$, Alice cannot get the reward $R$. For IRL, we fix $\epsilon$ and $w$ and infer $R$.

Suppose Alice chooses "wait" on Day 1. If she were fully rational, it follows that R (the preference for completing the task) is small compared to $w$ (the psychological cost of doing the tedious work). In other words, Alice doesn't care much about completing the task. Rational agents will do the task on Day 1 or never do it. Yet humans often care deeply about tasks yet leave them until the last minute (when finishing early would be optimal). Here we imagine that Alice has 9 days to complete the task and waits until the last possible day.

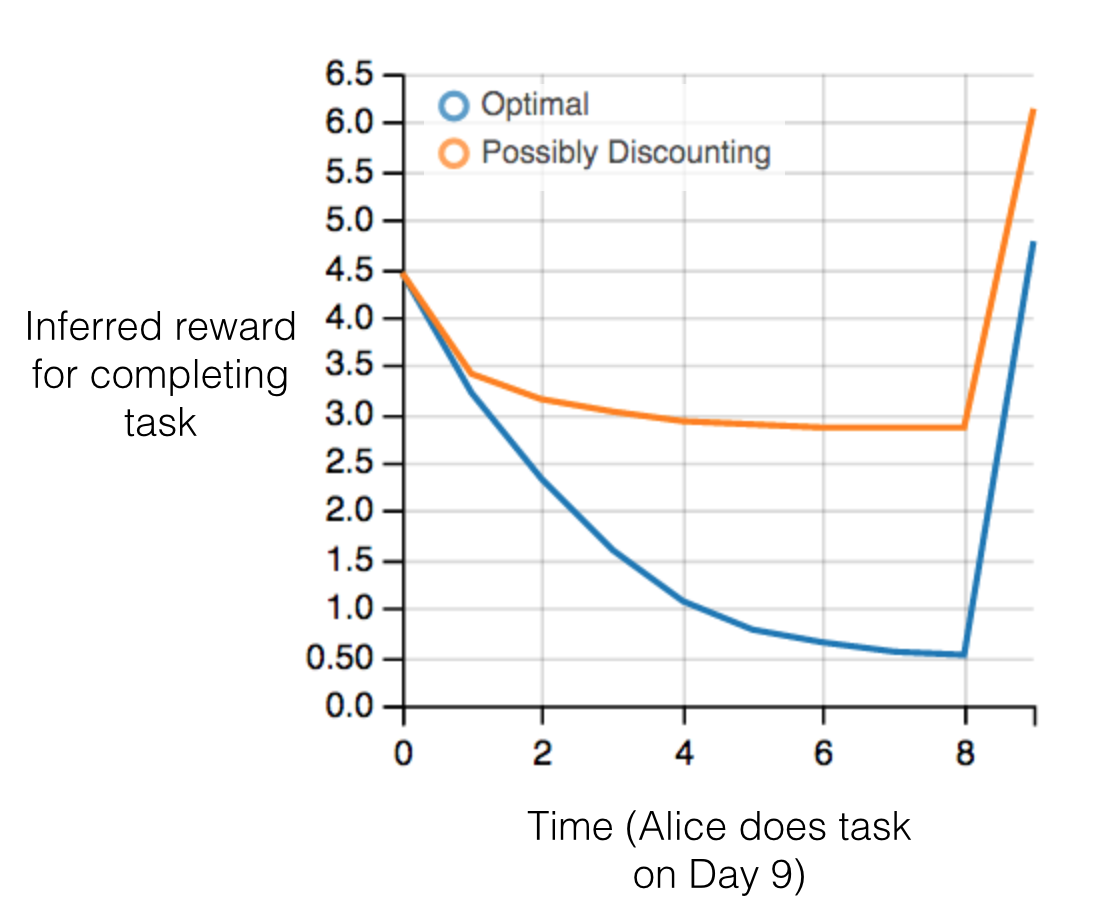
Figure 3: Graph showing IRL inferences for Optimal model (which is mis-specified) and Possibly Discounting Model (which includes hyperbolic discounting). On each day ($x$-axis) the model gets another observation of Alice’s choice. The $y$-axis shows the posterior mean for $R$ (reward for task), where the tedious work $w = -1$.

Figure 3 shows results from running IRL on this problem. There is an "Optimal" model, where the agent is optimal up to an unknown level of softmax random noise (a typical assumption for IRL). There is also a "Possibly Discounting" model, where the agent is either softmax optimal or is a hyperbolic discounter (with unknown level of discounting). We do joint Bayesian inference over the completion reward $R$, the softmax noise and (for "Possibly Discounting") how much the agent hyperbolically discounts. The work cost $w$ is set to $-1$. Figure 3 shows that after 6 days of observing Alice procrastinate, the "Optimal" model is very confident that Alice does not care about the task $(R < |w|)$. When Alice completes the task on the last possible day, the posterior mean on R is not much more than the prior mean. By contrast, the "Possibly Discounting" model never becomes confident that Alice doesn't care about the task. (Note that the gap between the models would be bigger for larger $T$. The “Optimal” model’s posterior on R shoots back to its Day-0 prior because it explains the whole action sequence as due to high softmax noise --- optimal agents without noise would either do the task immediately or not at all. Full details and code are here.)

Long-term Plans

Agents will often take long series of actions that generate negative utility for them in the moment in order to accomplish a long-term goal (for instance, studying every night in order to perform well on a test). Such long-term plans can make IRL more difficult for a few reasons. Here we focus on two: (1) IRL systems may not have access to the right type of data for learning about long-term goals, and (2) needing to predict long sequences of actions can make algorithms more fragile in the face of model mis-specification.

(1) Wrong type of data. To make inferences based on long-term plans, it would be helpful to have coherent data about a single agent’s actions over a long period of time (so that we can e.g. see the plan unfolding). But in practice we will likely have substantially more data consisting of short snapshots of a large number of different agents (e.g. because many internet services already record user interactions, but it is uncommon for a single person to be exhaustively tracked and recorded over an extended period of time even while they are offline).

The former type of data (about a single representative population measured over time) is called panel data, while the latter type of data (about different representative populations measured at each point in time) is called repeated cross-section data. The differences between these two types of data is well-studied in econometrics, and a general theme is the following: it is difficult to infer individual-level effects from cross-sectional data.

An easy and familiar example of this difference (albeit not in an IRL setting) can be given in terms of election campaigns. Most campaign polling is cross-sectional in nature: a different population of respondents is polled at each point in time. Suppose that Hillary Clinton gives a speech and her overall support according to cross-sectional polls increases by 2%; what can we conclude from this? Does it mean that 2% of people switched from Trump to Clinton? Or did 6% of people switch from Trump to Clinton while 4% switched from Clinton to Trump?

At a minimum, then, using cross-sectional data leads to a difficult disaggregation problem; for instance, different agents taking different actions at a given point in time could be due to being at different stages in the same plan, or due to having different plans, or some combination of these and other factors. Collecting demographic and other side data can help us (by allowing us to look at variation and shifts within each subpopulation), but it is unclear if this will be sufficient in general.

On the other hand, there are some services (such as Facebook or Google) that do have extensive data about individual users across a long period of time. However, this data has another issue: it is incomplete in a very systematic way (since it only tracks online behaviour). For instance, someone might go online most days to read course notes and Wikipedia for a class; this is data that would likely be recorded. However, it is less likely that one would have a record of that person taking the final exam, passing the class and then getting an internship based on their class performance. Of course, some pieces of this sequence would be inferable based on some people’s e-mail records, etc., but it would likely be under-represented in the data relative to the record of Wikipedia usage. In either case, some non-trivial degree of inference would be necessary to make sense of such data.

(2) Fragility to mis-specification. Above we discussed why observing only short sequences of actions from an agent can make it difficult to learn about their long-term plans (and hence to reason correctly about their values). Next we discuss another potential issue -- fragility to model mis-specification.

Suppose someone spends 99 days doing a boring task to accomplish an important goal on day 100. A system that is only trying to correctly predict actions will be right 99% of the time if it predicts that the person inherently enjoys boring tasks. Of course, a system that understands the goal and how the tasks lead to the goal will be right 100% of the time, but even minor errors in its understanding could bring the accuracy back below 99%.

The general issue is the following: large changes in the model of the agent might only lead to small changes in the predictive accuracy of the model, and the longer the time horizon on which a goal is realized, the more this might be the case. This means that even slight mis-specifications in the model could tip the scales back in favor of a (very) incorrect reward function. A potential way of dealing with this might be to identify “important” predictions that seem closely tied to the reward function, and focus particularly on getting those predictions right (see here for a paper exploring a similar idea in the context of approximate inference).

One might object that this is only a problem in this toy setting; for instance, in the real world, one might look at the particular way in which someone is studying or performing some other boring task to see that it coherently leads towards some goal (in a way that would be less likely were the person to be doing something boring purely for enjoyment). In other words, correctly understanding the agent’s goals might allow for more fine-grained accurate predictions which would fare better under e.g. log-score than would an incorrect model.

This is a reasonable objection, but there are some historical examples of this going wrong that should give one pause. That is, there are historical instances where: (i) people expected a more complex model that seemed to get at some underlying mechanism to outperform a simpler model that ignored that mechanism, and (ii) they were wrong (the simpler model did better under log-score). The example we are most familiar with is n-gram models vs. parse trees for language modelling; the most successful language models (in terms of having the best log-score on predicting the next word given a sequence of previous words) essentially treat language as a high-order Markov chain or hidden Markov model, despite the fact that linguistic theory predicts that language should be tree-structured rather than linearly-structured. Indeed, NLP researchers have tried building language models that assume language is tree-structured, and these models perform worse, or at least do not seem to have been adopted in practice (this is true both for older discrete models and newer continuous models based on neural nets). It’s plausible that a similar issue will occur in inverse reinforcement learning, where correctly inferring plans is not enough to win out in predictive performance. The reason for the two issues might be quite similar (in language modelling, the tree structure only wins out in statistically uncommon corner cases involving long-term and/or nested dependencies, and hence getting that part of the prediction correct doesn’t help predictive accuracy much).

The overall point is: in the case of even slight model mis-specification, the “correct” model might actually perform worse under typical metrics such as predictive accuracy. Therefore, more careful methods of constructing a model might be necessary.

Learning Values != Robustly Predicting Human Behaviour

The problems with IRL described so far will result in poor performance for predicting human choices out-of-sample. For example, if someone is observed doing boring tasks for 99 days (where they only achieve the goal on Day 100), they'll be predicted to continue doing boring tasks even when a short-cut to the goal becomes available. So even if the goal is simply to predict human behaviour (not to infer human values), mis-specification leads to bad predictions on realistic out-of-sample scenarios.

Let's suppose that our goal is not to predict human behaviour but to create AI systems that promote and respect human values. These goals (predicting humans and building safe AI) are distinct. Here’s an example that illustrates the difference. Consider a long-term smoker, Bob, who would continue smoking even if there were (counterfactually) a universally effective anti-smoking treatment. Maybe Bob is in denial about the health effects of smoking or Bob thinks he’ll inevitably go back to smoking whatever happens. If an AI system were assisting Bob, we might expect it to avoid promoting his smoking habit (e.g. by not offering him cigarettes at random moments). This is not paternalism, where the AI system imposes someone else’s values on Bob. The point is that even if Bob would continue smoking across many counterfactual scenarios this doesn’t mean that he places value on smoking.

How do we choose between the theory that Bob values smoking and the theory that he does not (but smokes anyway because of the powerful addiction)? Humans choose between these theories based on our experience with addictive behaviours and our insights into people’s preferences and values. This kind of insight can't easily be captured as formal assumptions about a model, or even as a criterion about counterfactual generalization. (The theory that Bob values smoking does make accurate predictions across a wide range of counterfactuals.) Because of this, learning human values from IRL has a more profound kind of model mis-specification than the examples in Jacob's previous post. Even in the limit of data generated from an infinite series of random counterfactual scenarios, standard IRL algorithms would not infer someone's true values.

Predicting human actions is neither necessary nor sufficient for learning human values. In what ways, then, are the two related? One such way stems from the premise that if someone spends more resources making a decision, the resulting decision tends to be more in keeping with their true values. For instance, someone might spend lots of time thinking about the decision, they might consult experts, or they might try out the different options in a trial period before they make the real decision. Various authors have thus suggested that people's choices under sufficient "reflection" act as a reliable indicator of their true values. Under this view, predicting a certain kind of behaviour (choices under reflection) is sufficient for learning human values. Paul Christiano has written about some proposals for doing this, though we will not discuss them here (the first link is for general AI systems while the second is for newsfeeds). In general, turning these ideas into algorithms that are tractable and learn safely remains a challenging problem.

Acknowledgments

Thanks to Sindy Li for reviewing a full draft of this post and providing many helpful comments. Thanks also to Michael Webb and Paul Christiano for doing the same on specific sections of the post.